A very short introduction to 64k demos

The demoscene features various demo competitions for modern systems. The most notable categories are PC demo, 64k intro and 4k intro.

For me, the followng two reasons have made me prefer 64k demos:

• it opens opportunities to implement a complex lighting solution, include interesting geometry, have multiple layers of post-processing.
• it keeps professional tools out for the most part, thus leaving technical problems for the group to solve.

What goes into a 64kb exe?

The minimum the program has to do is open a window, create a rendering context and setup a graphics pipeline. Depending on the rendering choices it might happen that geometry and textures are generated on the CPU and that there are many and complex rendering paths. This contributes to a fairly big code section.

More and more of the work has been pushed onto the GPU which is programmed through shaders. They are often stored in plain GLSL source code or D3D shader bytecode.

A music synthesizer of some sort and note data which will contribute to both the code and data sections.

The rest is an overhead coming from the used executable format and the amount of imported functions.

Considering that a "Hello world" program is already close or above this limit, one can begin to worry in one's success of developing a 64k intro. It turns out, it can be challenging but possible with some care and creativity.

If we could somehow create a 200kb executable and compress it into a 64kb executable, we would likely have more to show than an ordinary 64kb executable.

Here's a distribution of the three biggest sections in the uncompressed executable for our old intro Guberniya.

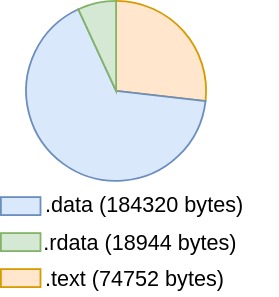
So, it's around 278 kb, most of which is data but not executable code.

To be able to enter the 64K category we would have to compress the executable in some way.

This is where a thing called an exe-packer comes into play.

What is an exe-packer?

An executable packer is a program which takes an Input program and outputs an Output program hopefully a lot smaller than the original one. The output program is still a binary executable and no unpacking to disk is necessary. The reduction of size is achieved through compression.

The machine code and data of the original executable are compressed through the use of a suitable compression algorithm. A small decompression stub becomes the entry point of the new program which will take the compressed data, decompress it somewhere in virtual memory, make some adjustments and jump into it to start the execution of the original program.

Many of the size-limited demos make use of .kkrunchy and Crinkler, correspondingly suited for 64KB and 4KB intros.

Almost all demo groups use them and both offer excellent compression rates and small decompression stubs.

Why write your own packer?

It's a cross of software engineering, low-level programming and science.

Working on the project wasn't about improving over other solutions but rather about learning and improving my skills. It helped me learn a lot more about data compression, how a PE32 binary looks like and a little bit about x86 assembly and its encoding.

Why 32-bit?

I preferred keeping some comfort when working on the project. Typically, a 64-bit executable is bigger than a 32-bit one, thus some extra effort might have been necessary into making it all fit. Compiled code for x86-64 will likely often include RIP-relative addressing which means that special care might be necessary to preprocess the data, so that it compresses better. Also, our existing engine had been developed in the mindset that it would be running as a 32-bit exe, so there were likely some incompatibilities (or bugs) which we did not want to resolve.

The compressor

Before going into details of each step, let me give you an overview of the pipeline.

• First we apply our domain knowledge to preprocess the data, so that it compresses better.
• We use LZ77 to compress the original data.
• We use a very simple adaptive 0-order model and arithmetic coder for the final pass.

LZ77

I stopped at LZ77 for its simplicity and good results. However, there are multiple other benefits I did not consider at the beginning.

First, it is an asymmetric compressor. The compressor might run slow since it has to find a good way to parse and encode the input. However, the decompressor is blazingly fast since it boils down to only memcopies and very few branches.

Second, in the limit of the string S with length N, the average bits/byte reaches the entropy of the source H(S)/N. Thus, with LZ77 we can still reach the absolute best we can do in terms of compression rate. The only issue is, of course, how fast we reach the limit.

LZ77 is really simple and the wikipedia page explains it really well. I will try to focus on the details of my implementation which helped me reach better results over time:

The three important parameters are the length and distance of references, and the minimum repetition length for which we would use a reference instead of directly copying the bytes into the output stream.

If the distance is too small, then we will not be able to use repetitions much earlier in the input. If too long, then we might be wasting bits in representing the distance.

If the length is too small, then we will not be able to handle very long repetitions with a single reference. If too big, again we will be wasting bits.

If the minimum repetition length is too small, then we will be wasting bits on encoding very short references. If too long, we will be directly copying data which could have been encoded through references.

I ended up selecting the following configuration:

• Distance: 16 bits. We would like to be able to refer to data much earlier in the input.
• Length: 8 bits. We do not expect to have very long repetitions. The length of a reference is thus at most 255.
• Minimum repetition length: 3 bytes (24 bits). Repetitions of length 3 or less can directly be copied.
• Type: 1 bit. We need it to disambiguate between references and direct copies.

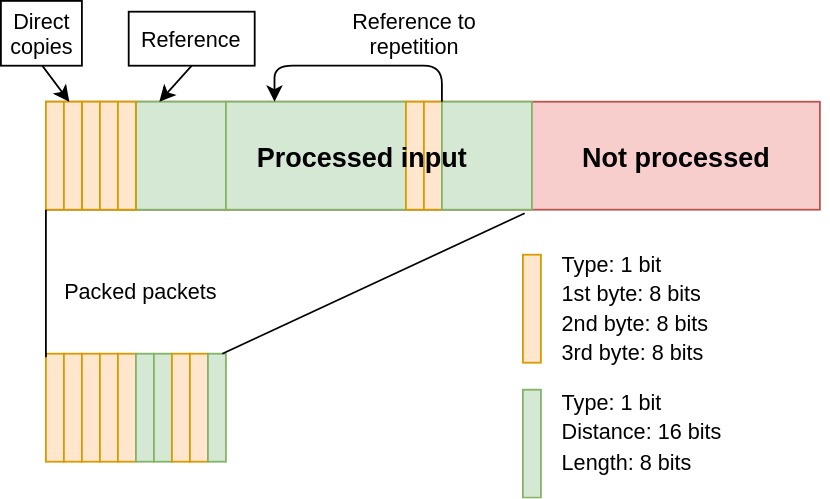
We can do a small optimization with respect to reference lengths.

If we are creating a reference, then we know that the repetition was bigger than 3. We can subtract (3+1) from the length of the repetition and use that instead. This adds the possibility to handle repetitions of 259 instead of the initial 255, thus saving some bytes potentially. This improved compression slightly.

An optimal parser assuming no entropy coding

We will be doing entropy coding afterwards, but let's assume that we won't. Thus the cost of a reference and direct copy will both be 25 bits.

How do we figure out when to use a reference and when to directly copy data, so that the total cost at the end is minimum?

We can try to design an algorithm linear in the input length using dynamic programming. Let's have an array best[] for which best[k] gives us the minimum cost for which we can parse the input from beginning till position k. Suppose we have somehow computed the minimum costs for each position up to k. How can we update the value for position k+1? Well, we can reach position k+1 in multiple different ways:

• Through a direct copy. Thus, from an earlier position we have copied 3 bytes and we have reached position k+1. This means that the cost would be best[k+1] = best[k-2] + 24 + 1 bits.
• Through a reference where the length could go from 4 to 259. Thus the cost would be best[k+1] = min(best[k-3], best[k-4], ..., best[k-258]) + 24 + 1 bits.

Since we can take either, the final cost becomes:

best[k+1] = min(best[k-2], best[k-3], ..., best[k-258]) + 24 + 1 bits

At the beginning we set best[0] = 0 and best[1...N] to infinity. We process the array from left to right keeping track of the selection which gave us the best result.

Once we are done processing the array, we can go from end to beginning to recover whether a reference or a direct copy should be made.

Filtering the code to improve compression

When addresses of functions are known during compile/link time, relative calls are used - one because it allows the binary to be a PIE, and two because absolute calls would require having the address be first stored into a register or read from memory in the form of an indirect absolute call. Thus, the majority of calls in our executable are relative calls. I measured that around 10% of the bytes in .text section are for relative calls - 1 byte op-code and 4 bytes offset.

Because the calls are relative, the 4-byte offset will vary since the call is always done from a different position in memory. We can transform the relative-offset into an absolute address by adding the address of the opcode. This guarantees that for every place where a given function is called, the op-code and now-transformed offset will match. That is a total of 5 bytes which will possibly repeat multiple times. The technique is known as the E8-E9 filter and more details can be found in this post by ryg.

Applying the E8-E9 filter yielded around 10% improvement in compression ratio which is huge given its simplicity.

Later the filter was replaced with .kkrynchy's disfilter. There was an improvement of around 6% over the E8-E9 filter.

Arithmetic coding

There wasn't anything special with regards how the arithmetic coder was implemented. I just followed the slides from a course I took in my B.S.

Designing a model

First some definitions:

The arithmetic coder needs to know the cumulative distribution of the symbols it has to encode/decode. For that we have to design a model which gives us a distribution which hopefully matches the actual distribution of the data we want to compress.

A static model is a model for which the probability of each symbol is pre-computed and stored. We cannot have a static model at all since the final binary has to be very small.

An adaptive model maintains the distribution of only the last K symbols. That distribution is likely closer to the distribution of the random variable which governs the next symbol in the stream.

I stopped at a 0-order adaptive model. A 0-order context would mean the model does not consider what any of the previous characters are to estimate what the probability of next symbol should be.

There were some complications in designing a model:

• When having an adaptive model, we run into the zero frequency problem. The solution, although bad, was to set the initial frequency of each symbol to 1. This means that we are paying a cost for symbols which might never occur.
• As mentioned before, the reference-distance is 16 bits. The distribution will be very sparse but we will still be paying due to the zero frequency problem. Moreover, we want to be able to update the distribution fast by either decreasing or increasing the frequency of the symbol. And we need the cumulative probability of a symbol. Thus, if we update the frequency of a symbol at the beginning (and this will happen often since the reference distance will often be small), then we have to update all the subsequent ~2^16 elements. A possibility is to use a Fenwick tree but the implementation will be slightly bigger thus making the decompresor bigger.

The solution was to split the 16-bit distance into two values - distance_low and distance_high. Each 8 bits.

This means two things: * The distributions of distance_low and distance_high will be less sparse and thus there would be less waste due to the 1 frequency initialization. * Updates and queries can be done naively but still be fast enough.

"Optimal" parsing

Yet another complication. Remember that optimal parser from before?

It's not optimal with respect to the output of the entropy coder. Why? - References will now likely no longer have a uniform cost of 25 bits. Some will be cheaper, some more costly. This would be the case with a static model as well. - Copied bytes will also no longer cost 25 bits. This would be true also for a static model. - We have an adaptive model, thus a choice at position i will change the distribution also effecting future choices. - Even if we know how to get the lowest cost up to a position i, there could be exponentially many different paths to reach that position with that cost. Every path could define a different distribution of symbols. The parser would have to use the formed distributions up to this point to know the best way to reach i+1.

So, we see it's an issue which affects compression rate. We also see that it's a computationally difficult problem. You can read this article from Cbloom for more info.

First, how do we compute the cost?

The entropy coder will output l number of bits per symbol where l depends on the probability p of that symbol. It turns out that the length l which minizes the average code word length is: l = -log2(p). The arithmetic coder will encode each symbol with length very close to the optimal one.

• The cost of a reference becomes: cost = -(log2(prob_distance_low) + log2(prob_distance_high) + log2(prob_length) + log2(prob_type_reference))
• The cost of a direct copy becomes: cost = -(log2(prob_symb_0) + log2(prob_symb_1) + log2(prob_symb_2) + log2(prob_type_copy)) where we also have to update the distribution after each of the symbols since we are using an adaptive model.

Since it's not clear which path is the best one and should be used, we can keep track of the first K-paths with the smallest cost to reach a given position. So, we have the possibly best K-paths for each index from 0 to R, then to compute the best K-paths for R+1 we can do the following:

def computeBest(i):
{
    struct Selection
    {
        cost = INF
        distribution = Empty
    }
    K_MAX = 256 // Keep at most 256 'best' paths.
    bestSelection[i] = MinHeap(K_MAX)
    // First try a reference
    for (j = 4; j < WindowMaxLength && j <= i; ++j)
    {
        if canReach(from = i-j, to = i)
        {
            cost, distribution = computeRefCost(bestSelection[i-jj], i)
            bestSelection[i].insert(cost, distribution)
        }
    }
    // Now try to copy bytes
    cost, distribution = computeCopyCost(bestSelection[i-3])
    bestSelection[i].insert(cost, distribution)
}

This improved the compression rate significantly!

Finishing the packer

As we have to generate our own executable, some knowledge of the PE32 format is necessary. The following two resources were enough to complete the packer. - Peering Inside the PE: A Tour of the Win32 Portable Executable File Format, Matt Pietrek - Understanding the Import Address Table

Duties of the packer and depacker

Using our compressor we can compress all of the sections of the original exe. Our decompressor stub will be the first thing executed in the new program. In order to guarantee that the new program produces the same output as the original, the depacker has the following duties:

• It should decompress the sections into the correct places in memory. We can figure out the correct addresses from the ImageBase field and each section's relative VirtualAddress field.
• It should handle imports. Since all of the sections of the original exe are compressed, the program loader would not know which are the imported libraries and functions. It becomes our responsibility to populate the Import Address Table.
• It should undo the code filter.
• Jump into memory where the original exe's entry point is.

A one-section exe

The new program will have exactly one big section. This potentially saves space as there are requirements on the alignment of each section in the file - 512 bytes. We also do not need more than one.

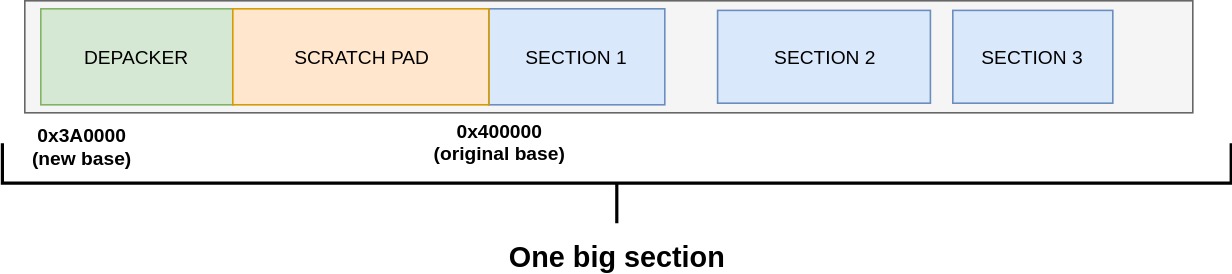
Since this one section serves for data and code, we will require that it's mapped with MEM_EXECUTE, MEM_READ and MEM_WRITE characteristic flags set. Since there are more possible characteristic flags and I did not know what I was doing, I decided that it's a safe bet to go over all sections and OR (|) the flags. This worked but it might not have been necessary or erroneous.

Let's say that all of the depacker is 0x1000 bytes long, that the uncompressed sections take 0xA1230 bytes, and that original ImageBase is 0x400000 (the default one).

Then we can have our new ImageBase as (0x400000-0x1000-0xA1230) & ~(PAGE_SIZE-1). We zero-out the last couple of bits due to page-alignment requirements. 0x1000 is reserved for the depacker stub. We are left with 0xA1230 bytes for scratch memory to decompress all of the sections. We can subtract more if we need more scratch memory.

Handling imports

As mentioned we have to handle imports. To do so, we can import a single library - KERNEL32.DLL - and two functions - LoadLibraryA and GetProcAddress. Our loader stub to handle imports can go over the Import Address Table (IAT), load the necessary libraries with LoadLibraryA and then call GetProcAddress to find the address of the functions necessary to import. Then we can update each IAT entry with the virtual address of the corresponding function.

Removing the DOS stub

Probably every PE32 article mentions that for legacy reasons many PE32 exes begin with a DOS header and executable code. We have to keep the header, at least most of it. We can remove the executable code as it will only be executed under DOS. This saves some bytes.

Better utilization of padding

Each section needs to be 512 bytes aligned. This means that there is likely empty space added for alignment before the section. We can take advantage of that to store additional information. There was around 192 bytes of unused space, so an optimization was to copy the last 192 bytes of the compressed data before the start of the section. Then in our depacker we can include a couple of instructions (e.g. rep movsb) to append the "hidden bytes" to the back of the compressed data.

Handling machine code

We have to include into our new executable the pieces of machine code for copying data, decompressing data and handling imports.

I wrote everything in C and used __declspec(noinline) to prevent the compiler from inlining the functions of my interest. I compiled using /Os to ask the compiler to produce smaller code if possible.

Then I used the Visual Studio debugger to get the machine code and instructions, copied them into a file and used a python script to generate a C byte-array which contains the machine code. Then I would copy the C array of bytes into my packer.

It's quite a cumbersome process. It would have been possible to use DUMPBIN and have a python script which does all of this automatically.

However, I did not have to go through the manual steps many times, so it wasn't that bad.

Final result

You can also download the exe from the download link in pouet. Note that it doesn't work on AMD.

The uncompressed exe has a size of 165 KB.

The compressed exe has a size of 62.1 KB which also includes the depacker stub.

I recall that was slightly worse than 7-zip's LZMA2 on maximum settings.

The demo was made with cce and msqrt.

Releasing the code and packer

I'm not releasing the packer. I'm not releasing the source code.

Here are the reasons:

• The packer is not on par with .kkrunchy or Ferris' squishy, so there's no use for it.
• The packer doesn't handle TLS and likely has bugs.
• The source code is a mess.

But if you have questions, write me an email :)

Acknowledgements

Thanks to Dmitry Kosolobov for answering my questions in our coincidental bumps on the busses in Helsinki.

And thanks to Juha Kärkkäinen for the excellent course on data compression.